
תוֹכֶן
- קבע את הזמן באוויר.
- שלב 1
- שלב 2
- שלב 3
- שלב 4
- קבעו את הגובה המרבי
- שלב 1
- שלב 2
- שלב 3
- קבע את המרחק האופקי שעבר.
- שלב 1
- שלב 2
- שלב 3
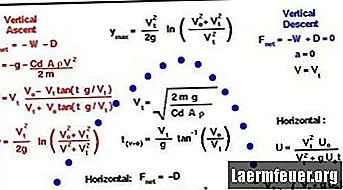
להלן שיטת חישוב מסלול הכדור ובאופן ספציפי את הזמן באוויר, הטווח והנקודה הגבוהה ביותר במסלולו. בדוגמה זו הושמעו כמה הנחות לפשט את החישוב: התנגדות אוויר זניחה, אין רוח ומרחק ירי לא מספיק כדי שהסיבוב של כדור הארץ ייכנס לתוקף.
קבע את הזמן באוויר.
שלב 1
ראשית, יש לקבוע את צורת הקשת. אם הזווית תחילה כלפי מטה, הרי שכבר ידוע שהנקודה הגבוהה ביותר היא עמדת הירי. גם בזווית כלפי מעלה יכולה המטרה להיות הנקודה הגבוהה ביותר, בין אם זווית זו רדודה ובין אם גובהה מספיק (h). ניתן לקבוע זאת בשלב רביעי, כאשר נקבע זמן האוויר.
שלב 2
אם הזווית "?" קצב הירי הוא זה שבין המסלול הראשוני של הקליע לאופקי, כך שהמהירות האנכית הראשונית היא V (i) = V.sen?.
שלב 3
זמן אוויר נמצא באמצעות משוואת המיקום h = V.sen? .T - (0.5) g.t ^ 2, כאשר g = 9.8 מטר / שניות ^ 2. כל המשתנים ידועים, למעט הזמן באוויר, t, כך שניתן לפתור זאת באמצעות הפונקציה הריבועית: ax ^ 2 + bx + c = 0, לכן, x = [-b ± √ (b ^ 2-4ac )] / 2 א
שלב 4
אם מותר יותר מפתרון אחד ל- t, מכיוון ש h> 0, התוצאה הראשונה מתאימה כאשר גובה = h בנתיב העלייה, והשני ל כאשר גובה = h בנתיב הירידה. אם h <0, אז הפיתרון האמיתי היחיד עבור t הותר, והשני הוא שלילי.
קבעו את הגובה המרבי
שלב 1
אם? <0, אז כבר ידוע שהגובה המרבי הוא הגובה ההתחלתי, h = 0.
שלב 2
אם הייתה יותר מפעם אחת, t, בה הכדור משתרע על h, אז הקטן ביותר t מתאים לנתיב טיסה שבו h היא הנקודה הגבוהה ביותר. T הגדול ביותר תואם את הכדור שמגיע לגובה גבוה יותר לפני שהוא חוזר ל- h, כדי לפתור את הגובה הזה, הנוסחה V (t) = V (0) - 9.8t משמשת למציאת הערך של t כאשר המהירות האנכית היא אֶפֶס. במילים אחרות, באיזו שעה, t, V.sen? = 9.8t.?
שלב 3
לפתור t ולחבר את נוסחת הגובה, יש לנו את הגובה המרבי: hm = V.sen? - 4.9 ט ^ 2. אותה גישה משמשת לפתרון גובה מרבי, אם מותר רק פיתרון אחד ל- t.
קבע את המרחק האופקי שעבר.
שלב 1
כדי לקבוע את המרחק האופקי שעובר עד שהכדור מגיע לגובה h, תחילה תחשב את המהירות האופקית הראשונית של הכדור: v (i) = V.cos (?).
שלב 2
החלף את הזמן, t, כאשר הכדור מגיע לגובה הסופי, A, במיקום הנוסחה באמצעות מהירות אופקית: A = V.cosΘ.t. בהנחה שאין התנגדות אוויר ואין מונח תאוצה בצד ימין.
שלב 3
אם הייתה יותר מפעם אחת t כאשר הגובה היה ב- h, אז שתי המיקומים של "A" יהיו תקפים, כאשר הנקודה הגבוהה ביותר שהושגה היא hm עבור הקטן מבין השניים "A". עמדות הקצה האופקיות והאנכיות והנקודה הגבוהה ביותר שהושגו ידועות כעת, ובכך קובעות את מסלול הכדור.