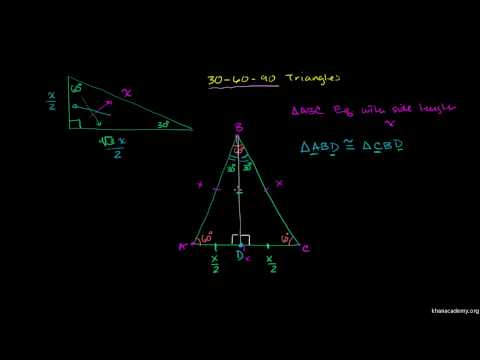
תוֹכֶן
המשולש הוא מצולע תלת-צדדי. סכום הזוויות שבהן נפגשים הצדדים הוא תמיד 180 מעלות. לזוויות של כמה משולשים יש תכונות מיוחדות המזהות את המשולש כמו של סוג מסוים. לדעת את המאפיינים של זוויות של משולש שימושי לחישובים בבנייה, גיאומטריה, כיוון, ניווט ונושאים רבים אחרים.

משולשים מלבניים
למשולש הימני יש זווית של 90 מעלות, הידועה כזווית הנכונה. יש לו שני צדדים צדדיים ואת סכום של שתי זוויות אחרות שלה טופס 90 מעלות. לדוגמה, נניח שאחת הזוויות היא 60 מעלות והשאר 90 מעלות. הזווית השלישית צריכה להיות שווה 30 מעלות, שכן סכום הזוויות של המשולש הוא 180 מעלות.
ישנם שני משולשים מלבן מיוחד. אחד עם זוויות של 30, 60 ו 90 מעלות והשני עם שתי זוויות של 45 מעלות ואחד של 90. משולש של 30, 60 ו 90 הוא חצי מלבן; בעוד אחד 45, 45 ו 90 הוא חצי ריבוע. שניהם נמצאים על ידי חלוקת ריבוע או מלבן בפינות ההפך.
משולש של איסוסל
לפחות שני זוויות של משולש משקפיים יש ערך זהה. המשולש של 45, 45 ו -90 מעלות הוא איסופל ומלבן בו זמנית, אבל לא כל המשולשים הם משולשים. משולש עם זווית של 70 מעלות ושני זוויות אחרות של 55 מעלות, למשל, הוא משולש שהוא isosceles ולא מלבן.
חלוקת הזווית העליונה - הנקראת פסגה - שווה ומרחיבה קו לבסיס, יוצרת שני משולשים מלבנים זהים עם זווית השיא כמחצית מהמקור, זווית נוספת של 90 מעלות וזווית שלישית שנותרה זהה לזו של המקור .
משולש שווה צלעות
כל שלוש הזוויות של המשולש המשולב הן זהות: 60 מעלות. אורכן של הצדדים של כל המשולש קשורה ישירות זוויות שלהם, וזה מה שעושה את משולשים חד צדדיים מיוחדים. היחס בין הזוויות הוא 1 עד 1; ואת היחס בין הצדדים הוא גם 1 עד 1, כלומר, הצדדים שלהם זהים.
קו משורטט בזווית הקצה של משולש שווה צלעות בניצב לבסיס ירכיב שני מלבנים עם אותן זוויות. מאפיין זה של זוויות משולש שווה צלעות הופך אותו למשולש איסוסל, בנוסף למשולש שווה צלעות.
משולשים לא סדירים
משולש לא סדיר יש זוויות כי סכומי שלו לגרום 180 מעלות, כמו כל המשולשים, אבל אין להם שתי זוויות שוות ולא זווית של 90 מעלות. זווית הפסגה שלה ניתן לחלק על ידי ציור קו מאונך לבסיס. קו זה יהווה שני מלבנים בגדלים שונים. תכונה זו מאפשרת זוויות של משולש לא סדיר להיות מחושב באמצעות מתמטיקה עבור משולשים מלבניים אם לפחות זווית אחת בצד אחד או גובה ידועים.
מתמטיקה של מלבן המשולש
זווית הצדדים של המשולש ניתן לחשב בשיטות רבות. אם אתה יודע שתי זוויות, השלישי ניתן למצוא על ידי הפחתת הסכום ביניהם על ידי 180. לדוגמה, משולש עם שתי זוויות כי הסכום נתן 114 מעלות, יש את הזווית השלישית שווה 66 מעלות (180 - 114 = 66).
זוויות המשולש הימני קשורות במישרין למידותיהן. לדוגמה, היחס של הצד הנגדי של המשולש אל הצד הסמוך לזווית נקרא משיק. באמצעות שולחן או מחשבון עם פונקציות טריגונומטריות, אתה יכול בקלות למצוא את הזווית. כמו כן, היחסים בין הצד הסמוך של זווית עם hypotenuse שלו נקרא הקוסינוס ואת היחס של הצד הנגדי כדי hypotenuse ידוע בשם סינוס.